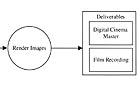
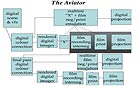
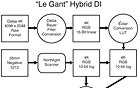
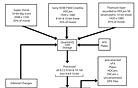
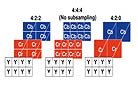
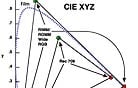
In the same way that analog audio is digitized, the analog film’s RGB frequency waves are sampled, which measures the intensity at each location and forms a two-dimensional array that contains small blocks of intensity information for those locations. Through the process of quantization (analog-to-digital conversion), that data is converted by an imaging device to integers (natural numbers, their negative counterparts, or 0) made up of bits (binary digits). Each pixel is assigned specific digital red, green and blue intensity values for each sampled data point. This is color bit depth. Usually for imaging, integers are between 8 and 14 bits long but can be lower or higher. For example, if the stored integer is 10 bits, then a value between 0 and 1023 may be represented. The higher the bit rate, the more precise the color and the smoother the transition from one shade to another. If an image is quantized at 8-bit color bit depth, each component’s integer will have a value that is 8 bits long. The higher the bit depth, the more sample points, the fewer the artifacts. Scanners and telecines today operate at bit depths ranging from 8 to 16 bits per color component (see diagram).

A further consideration is how to stack the representations of intensity to represent the color values of the scene. This stacking is known as the “transfer function,” or characteristic curve of the medium. In the physical world of film, the transfer function is fixed when the film is manufactured and is determined by the sensitivity of the film to light in the original scene.

Human vision is more sensitive to spatial frequency in luminance than in color, and can differentiate one luminance intensity value from another as long as one is about one percent higher or lower than the other. The encoding of these luminances is done in either a linear or nonlinear fashion. The term “linear” has been used somewhat erroneously in the industry to describe encoding methods that are quite different from each other. In the most common of these usages, linear (as in a “log to lin conversion”) actually refers to a form of power-law coding.

Power-law coding is not pure linear, but not quite logarithmic either. It is a nonlinear way of encoding done primarily in the RGB video world at 8 bits, 10 bits for HDTV as stipulated in Rec 709. The code values for RGB are proportional to the corresponding light coming out of a CRT raised to a power of about 0.4. If your eyes are now starting to glaze over, that’s understandable. This is the type of equation taught in the higher math class that might have been skipped.

The other method of encoding commonly described as linear is the representation of scene intensity values in a way that is proportional to photons. (To put it simply, a photon is a unit of intensity of light.) In other words, a one-stop increase in exposure doubles the photons, and hence would double the corresponding digital value. Visual-effects artists prefer to work in this scene-linear space because it seamlessly integrates with their like-valued CGI models.

Although the way human vision recognizes light intensity and the way film records light can be modeled either by logarithm or by power-law, “neither description is completely accurate,” points out Walker.

Matt Cowan, co-founder of Entertainment Technology Consultants (ETC) notes: “For luminance levels we see in the theater, we recognize light intensity by power-law. Film actually records light by power-law, too; the transmission of film is proportional to the exposure raised to the power gamma. Film-density measurement is logarithmic, but we do that mathematically by measuring the transmission, which is linear, of the film and converting to density, or D = log(1/T), where the log transformation is not inherent to the film.”

Logarithmic, power-law and linear. To avoid any possible confusion — if it’s not too late — I will speak mostly in logarithmic terms, because they are used more often to describe photography.

Film is measured in logarithmic units of optical density, something that Kodak used in its Cineon system. (Just look at a sensitometric graph —the X-Y axes are respectively log-exposure and density, a form of log.) The values are proportional to the negative’s optical density, and this ensures that more of the encoded values will be perceptually useful as exposure to light increases. Although different density standards have been used to measure density on a negative, such as the ISO standard status M, the Cineon system introduced the use of printing density, which is based on the spectral sensitivity of the print material and the light source used for exposure. For a particular film, printing density is analogous to the way the print film sees the negative film. This allows for a more accurate simulation of the photographic system in the digital world. Using the same concept of printing density to calibrate the scanner and film recorder to an intermediate film stock allows accurate reproduction of the original camera negative, regardless of which film stock was used.

Currently in the DI, 10-bit log is common, though some feel 12-bit log is a sufficient level of encoding that should be supported internally within DI pipelines. The SMPTE DC28 digital cinema committee found that 12 bits used with a 2.6 power-law coding in RGB adequately covers the range of theater projection expected in the near future (see diagram). Again, this could be another one of those myopic instances. Lou Levinson, senior colorist at Post Logic and chair of the Technology Committee’s Digital Intermediate subcommittee, has greater aspirations: “What I am going to propose as the optimum pipeline is that you have a very high bit depth backbone — XYZ bits, 16 bits per channel minimum — and that it’s bipolar. Rather than counting from 0 and going all the way up to 1, I’m going to make the middle 0 and then plus or minus how many bits you have. So if you have 16 bits and 0 is middle grade, then you can go all the way to +15 bits and –15 bits. There are lots of reasons why I like having 0 in the middle because certain things fail to 0. When they stop working, they won’t add or subtract anything bad to the picture.”

When the bits are calculated to create and display an image file, one can choose to have those computer calculations performed as straight integer quantities or as floating point. Current computers process at 32 or 64 bits, with 32 being more widely supported. Now this is a computer microprocessing bit rate; these bits are different than color bits. Calculating as integers is often a faster process, but it can lead to errors when the calculation rounds up or down to an incorrect integer, thereby throwing the value of the RGB components off. Floating point is a somewhat slower but more precise method of rounding because it allows for decimal fractions (the floating “point”), leading to fewer errors. The color shift that results from an error is generally too small to perceive. Instead, what is seen are artificial structures or edges that have been introduced into the image known as banding, which disrupts the smooth color gradient. The same banding also can be caused by low color bit depth.

We humans value detail and sharpness more than resolution in an image. High resolution is synonymous with preservation of detail and sharpness, but high pixel count does not always translate into high resolution. “As you try to increase the amount of information on the screen,” explains Cowan, “the contrast that you get from a small resolution element to the next smallest resolution element is diminished. The point where we can no longer see [contrast difference] is called the limit of visual acuity.” (see diagram) It’s the law of diminishing returns, and a system’s ability to preserve contrast at various resolutions is described by the modulation transfer function (MTF). The eye is attuned to mid-resolution information, where it looks for sharpness and contrast. A higher MTF provides more information in the mid-resolution range. You just want to make sure that the resolution doesn’t drop so low that you pixellate the display, which is like viewing the image through a screen door (see diagram).

All of the encoded values must be contained within a storage structure or file. A number of file formats exist that can be used for motion imaging, but the most common ones being transported through the DI workflow are Cineon and its 16-bit capable offshoot DPX (Digital Motion-Picture eXchange in linear or logarithmic), OpenEXR (linear) and TIFF (Tagged Image File Format in linear or logarithmic). All of these formats contain what is known as a file header. In the header, you and whatever piece of electronic gear that is using the file will find grossly underutilized metadata that describe the image’s dimensions, number of channels, pixels and the corresponding number of bits needed for them, byte order, key code, time code … and so on. Fixed-header formats such as Cineon and DPX, which are the most widely used as of right now, allow direct access to the metadata without the need for interpretation. However, all information in the fixed headers is just that — fixed. It can be changed, though, but with great effort. These two formats do have a “user-defined area” located between the header and the image data proper, allowing for custom expansion of the metadata.

TIFF has a variable header, or Image File Directory (IFD), that can be positioned anywhere in the file. A mini-header at the front of the TIFF file identifies the location of the IFD. “Tags” define the metadata in the header, which has room for expandability. Open EXR, a popular visual-effects format which originally was developed by Industrial Light & Magic for internal use, also is a variable-header format.

“You can convert from one format to another,” says Texas Instruments’ director of DLP Cinema Technology Development Glenn Kennel. Kennel chairs the Technology Committee’s Digital Display subcommittee and worked on the original Cineon system while at Kodak. “The important thing, though, is that you have to know enough information about the image source and its intended display to be able to make that conversion. What’s tricky is whether the color balance is floating or the creative decisions apply to the original image source. If the grading has been done already then you have to know the calibration of the processing and display device that was used.”