Moiré and the Fashion of Harry Nyquist 

When a costume designer brings a swatch of material or an early wardrobe sample to a cinematographer to ask whether it will work for camera, they are inquiring, of course, about the hue and reflectivity of the material — but they are also asking, though probably not in so many words, “Will this texture exceed the Nyquist limit of your digital camera system and cause a moiré pattern on the screen?”

Even as most costume designers are unlikely to use that specific terminology, they’re aware that certain materials (and certain patterns) will cause moiré, and that this is a significant issue. Likewise, many cinematographers don’t have the Nyquist-Shannon sampling theorem on the tip of their tongue, nor would they necessarily conceive of the moiré phenomenon as an interference pattern caused by conflicting spatial frequencies in relation to the photosite count of a particular digital sensor — but they generally, instinctively know what will or will not cause moiré.

This month’s Shot Craft will investigate the Nyquist-Shannon sampling theorem to clarify what causes moiré in a particular textile or pattern, and how to avoid it. 

Definitions and Measurements
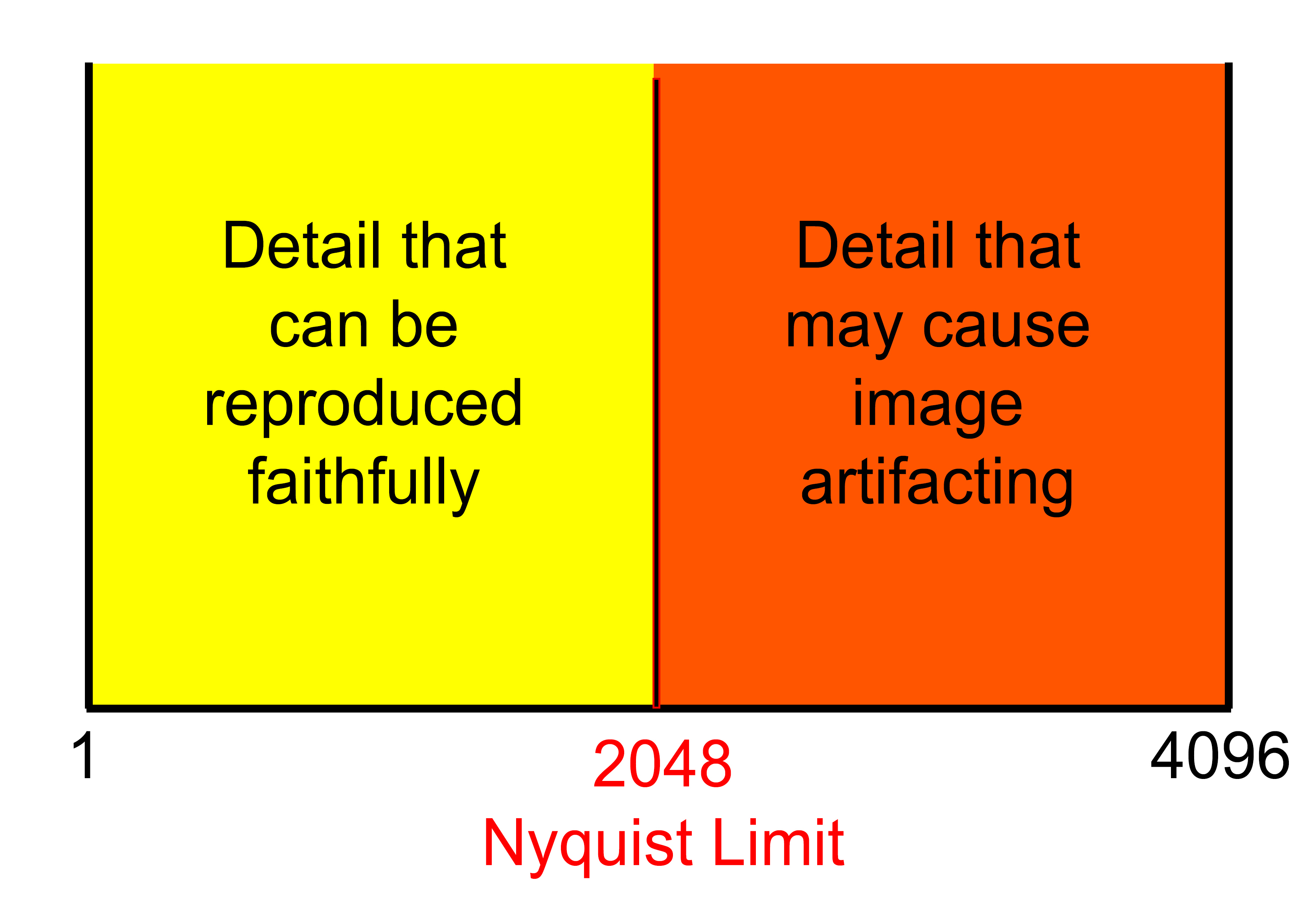
Harry Nyquist was a Swedish physicist and electronic engineer who conducted R&D at AT&T from 1917 to 1934. His research into reproducing sound signals, which was expanded upon by American mathematician and electrical engineer Claude Shannon, has come to be known as the Nyquist-Shannon sampling theorem. This theorem states that for any given sampling system, the maximum detail that can be faithfully reproduced is half the number of samples taken. Although Nyquist and Shannon were referencing audio samples, the same concept applies to images sampled by a digital sensor. To produce a digital image of a real-world subject, every photosite on the digital sensor takes a sample of the photons of light reflecting off the objects being photographed. By applying the Nyquist-Shannon theorem, we conclude that the maximum image resolution that can faithfully be reproduced is half the number of samples captured by the photosites.

To determine resolution — that is, the system’s ability to resolve detail — there must be two high-contrast elements in order to see the difference between them. To accomplish this, we use a series of Ronchi grates (or Ronchi charts), each of which comprises a row of black lines on a white background, with each successive grate featuring narrower lines with a decreasing distance between them.

“If we try to photograph a pattern that exceeds what the camera system can reproduce, this will introduce image artifacting that presents itself as moiré.”

If we consider the white space between each black line to be a line in itself, and we take into account the Nyquist-Shannon theorem — which indicates that the maximum number of lines any digital camera system can reproduce is half the number of its sensor’s photosites — then it can be concluded that a camera system with 4,096 photosites across the imager can give us a maximum of 2,048 lines. (Granted, this is a simplification of the Nyquist-Shannon sampling theorem, but it aptly illustrates this important aspect of the sensor. We’re also keeping things simple by looking only at an example dealing with black and white; reproducible resolution in color, which typically involves subsampling with a Bayer-pattern color-filter array, is a subject for another column.)

Those 2,048 lines equate to a real-world physical measurement, defined by line-pairs per millimeter (or lp/mm). If the sensor is 36mm wide, and we can resolve detail down to 2,048 lines, the measurement is 57 lp/mm (2,048 divided by 36mm). This measurement can also be called a spatial frequency, referring here to the frequency of respective black and white lines within 1mm of space. That’s the finest detail the camera system can reproduce without artifacting. The system is capable of faithfully reproducing any detail larger (at a lower spatial frequency) than 57 lp/mm. 

Causes of Moiré
So, what happens when we try to photograph a pattern that exceeds what the system can reproduce? In other words, what if we violate the Nyquist limit of the system? If this is a repeating pattern of high-spatial-frequency fine detail — like one might find in a woven fabric — then, given the specific parameters above, any detail smaller (at a higher spatial frequency) than 57 lp/mm will end up introducing image artifacting that presents it-self as moiré.

If moiré is recorded by the camera, it cannot be easily removed from the image in postproduction. There are no hardware or software tools in post that achieve this, so — barring a reshoot — the object in question must be replaced by a moiré-free CG version of the object. The seriousness of the moiré issue helped lead digital-camera manufacturers to incorporate an optical low-pass filter (OLPF) into their cameras. This filter allows low spatial frequency to pass through the quartz filter while blurring high spatial frequency above the Nyquist limit for that specific sensor. 

The OLPF does not always eliminate moiré, however, which is why cinematographers and costume designers must carefully consider the textile patterns that will be presented on camera. The likelihood of moiré is affected by the number of photosites on the sensor, as discussed, and also by the contrast of lighting, the re-solving power of the individual lens, the compression algorithm of the recording format, and the compression algorithm of the postproduction delivery format. The cinematographer must consider all these points in the workflow to ensure that no moiré is ever captured on camera.

One particular complication is that moiré can appear on a monitor that is downsampling the resolution of the camera even if the artifact is not actually recorded in the image itself. If your camera has 4,096 photosites across the sensor but you’re assessing the image on a 1,920-pixel monitor, the Nyquist limit of the monitor is significantly lower than that of the camera (960 as opposed to 2,048), which means the image will moiré on the monitor long before it will on the camera. The best way to check is to use a monitor with a 1:1 pixel function to magnify the image so that it is in parity with the camera’s sensor. 

“If moiré is recorded by the camera, it cannot be easily removed from the image in postproduction.”

Moiré Solutions
If you end up working with a textile that is causing moiré and there is no way to replace it with a different material, there are several things you can try. Moving the camera slightly closer to the subject or shifting to a tighter focal length, thus increasing the size of the pattern in the frame — and removing the resonance between the textile pattern and the digital sensor — can help eliminate moiré. You can also move the camera slightly farther away from the pattern or shift to a wider focal length, thus removing the ability of the sensor to discern the fine detail that’s causing the issue.

If you really need the precise shot that’s causing the moiré problem, you can increase the sampling size (or number of photosites on the sensor) by switching to a larger-format camera. An 8K sensor with 8,192 photosites across the imager, for example, will have a Nyquist limit of 4,096. If we assume the same 36mm width of this sensor as submitted above, then the finest detail the system can reproduce is 114 lp/mm — twice as fine as a 4K imager. 

Aliasing in the Eye
The Nyquist limit is not confined to digital sensors. The human eye has a Nyquist limit, too; there is a finite spatial frequency our eyes can resolve before we see aliasing. When you look at the fine pattern of a window screen, for example, you might notice a wavy variation of contrast that “swims” when you move your head slightly. That’s moiré happening in your eye because the spatial frequency of that pattern violates your Nyquist limit. If you step closer to the screen, the moiré might disappear. That’s because the spatial frequency of the pattern you’re looking at has dropped because you have moved closer to it, and the pattern subtends a larger angle on your retina. In essence, by moving closer, you have reduced the spatial frequency of the window screen according to your eye.

LED Walls and Moiré
Another situation in which the Nyquist-Shannon sampling theorem rears its head, and one that is becoming more common, is when digital cameras photograph LED walls. LED walls comprise a finite pattern of pixels — an isotropic grid — and this rigid geometric pattern of pixels has its own fixed spatial frequency. Therefore, when the camera focuses on the LED screen, it can cause significant moiré in the image. The finer the pixel pitch of the screen and the higher the photosite count of the sensor, the less chance there is of seeing moiré, and, generally speaking, the farther away and the more out of focus the LED screen is, the less likely you are to encounter it.

Jay Holben is an ASC associate member and AC’s technical editor.

You’ll find all Shot Craft posts here.