Revisiting — and Updating — Inverse-Square Law

Photos by Jay Holben unless otherwise credited.

Inverse-square law is a bit of physics that is central to the cinematographer’s craft, which describes how light loses intensity over the distance it travels — and it’s time to take a new look at it.

Look at a point source: Light emanates from it in all directions simultaneously, and the farther that light travels, the dimmer it gets. This is because as the rays of light travel, they diverge and spread. Imagine the point source as a tiny sphere of light, and as light travels away from the source, that sphere expands in size, like a balloon, so the surface area grows. As the balloon of light expands, so does the area over which the light spreads — covering an increasing area at decreasing brightness.

As the figure below shows, light rays diverge from a point source. At 1', that light covers a theoretical 1'-square area; at 2', that same light will be spread over a 4'-square area, and at 3', that same light will spread over a 9' square area. If the illustration continued to 4' distance, we’d see the light spreading over 16 square feet. So, from 1' to 4', the light drops in intensity to 1/16 of its initial brightness.

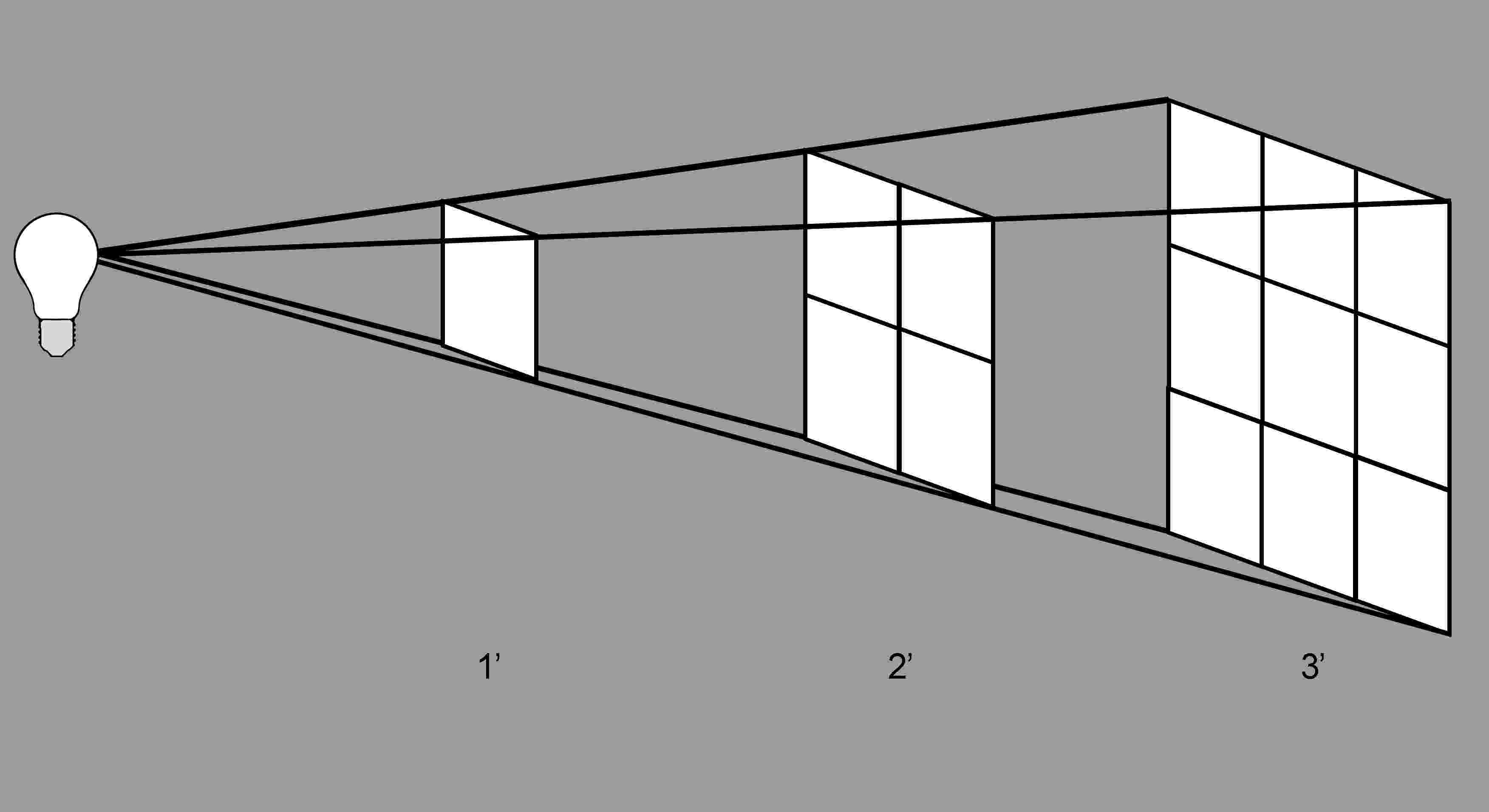
What we can see is that light does not lose intensity linearly, but rather logarithmically. Moving a source twice as far from a subject is not half the brightness, but one quarter. (The intensity is reduced by the square of the distance traveled). Starting our measurement at 1' away from the source as the reference, at 2', the light will be ¼ that intensity; at 4', it will be 1/16, and at 8', it will be 1/64.

Another way to look at this is to say that, in general, light from a point source will drop 1 stop in intensity at an increase of half the distance (relative to a reference) away, and 2 stops in intensity at twice the distance away. If we move a lamp that’s 1' from a subject back to 1.5' (or if the subject moves away from the lamp), the light loss will be ½ the intensity, or 1 stop. If we move that fixture 2' away, the light loss will be ¼ or 2 stops. The same is true if we move a light from 10' to 15': the loss is 1 stop. From 10' to 20', the loss is 2 stops.

When plotting this out on a chart, something interesting emerges. The falloff, due to its logarithmic nature, starts extremely steep, with substantial loss over a short distance, but then it starts to level out. The farther you are from the source, the less loss of light there is over a given distance. So, from 1' to 2', you have ¼ the intensity of light — a loss of 75 percent! — but from 7' to 8', you have a loss of 13 percent.

So, if one subject is 1' away from a light source and another subject is 2' away from the same source, the latter subject will be 2 stops darker than the former. But if a subject is 7' from a source and another subject is 8', then the subject at 8' will be only slightly darker; in fact, the difference will be mostly unnoticeable to the eye.

This also works for lighting groups of people: The farther away the source is from subjects, the more evenly the light will spread among them.

Inverse-square law is also very helpful in determining how bright a source you will need for a given setup. Knowing the photometrics of a source and the distance at which you will set it in a given setup will tell you the intensity of the light on the subject and whether or not you’ll need a 2K, 5K or 20K to get the exposure you require at the distance you’re working with.

This works two ways. If there’s a fixed relationship between your fixture and your subject, then using inverse-square law can aid in determining the size of fixture necessary to light your subject to a specific stop. And if your fixture is providing too much intensity, knowing inverse-square can help you quickly determine how much light you can reduce by simply increasing the distance between source and subject.

The Caveat
In all the textbooks, there’s a caveat to inverse-square law: It only applies to point sources. Once you increase the size of the source to a soft light, the physics no longer apply.

This has been a universally accepted truth for ages.

But not too long ago, Tim Kang, a cinematographer and associate member of the ASC, told me he had a theory about how inverse-square law would apply to soft sources. Kang is the principal engineer of color and imaging for Quasar Science, and he chairs the ASC MITC Lighting Committee. Naturally, I was intrigued and excited to put his theory into practice.

On a Triscenic soundstage, secured for the day with generous assistance from MBS Equipment Co. and Triscenic Production Services, we gathered to prove (or disprove) Kang’s theory with practical testing. (See the test setup below) Joining us were gaffer Mike Visencio — the senior vice president of technology and innovation for the MBS Group — and cinematographer Kaity Williams.

Kang’s theory is that the physics of inverse-square does apply to soft sources, but not until the source and the subject are apart by a distance equal to that of the widest width of the source. At distances closer than that, inverse-square does not apply.

(The “widest width” is the diameter for a circular source and the diagonal for a square or rectangular source. To find the diagonal of a quadrilateral shape requires the Pythagorean theorem: a2+b2=c2 where “a” is the length of one side, “b” is the length of the perpendicular side and “c” is the diagonal.)

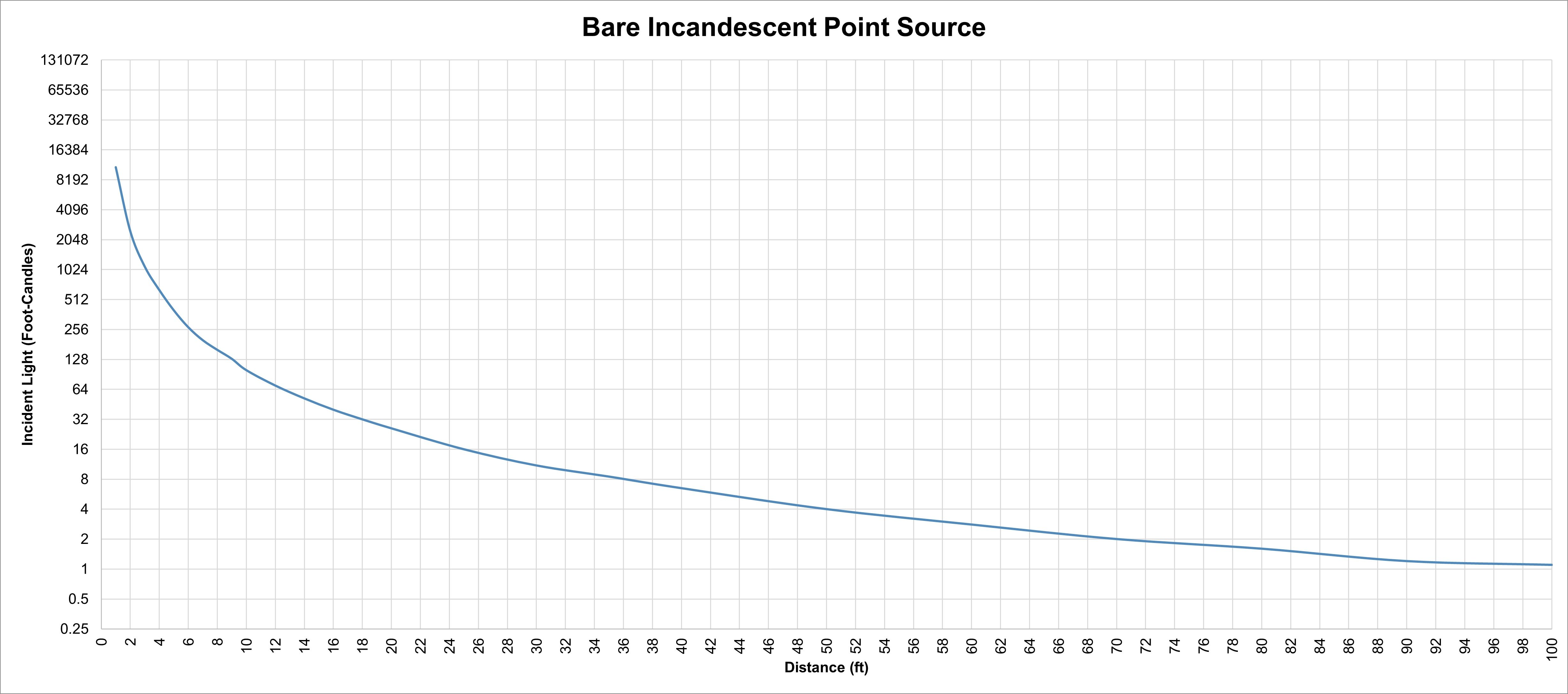
We tested the theory with a control of a point source (an open-face 2K), a 6'x6', a 12'x12' and a 20'x20' — measuring footcandle intensities at distances from 1' to 100'.

Each source was isolated as much as possible to prevent reflections or corruption of light, but this was nevertheless a real-world setting — not a laboratory environment — where tight precision is very difficult, if not impossible, to pro-duce. In fact, even our control source, the 2K, didn’t result in perfect readings along the mathematical ideal. But, in the end, we found that Kang’s theory holds true: inverse-square law can be applied to soft sources!

The Proof
See the charts below and on the facing page.

The first chart shows our measurements from the control — a 2K Junior with the Fresnel open and out of the way.

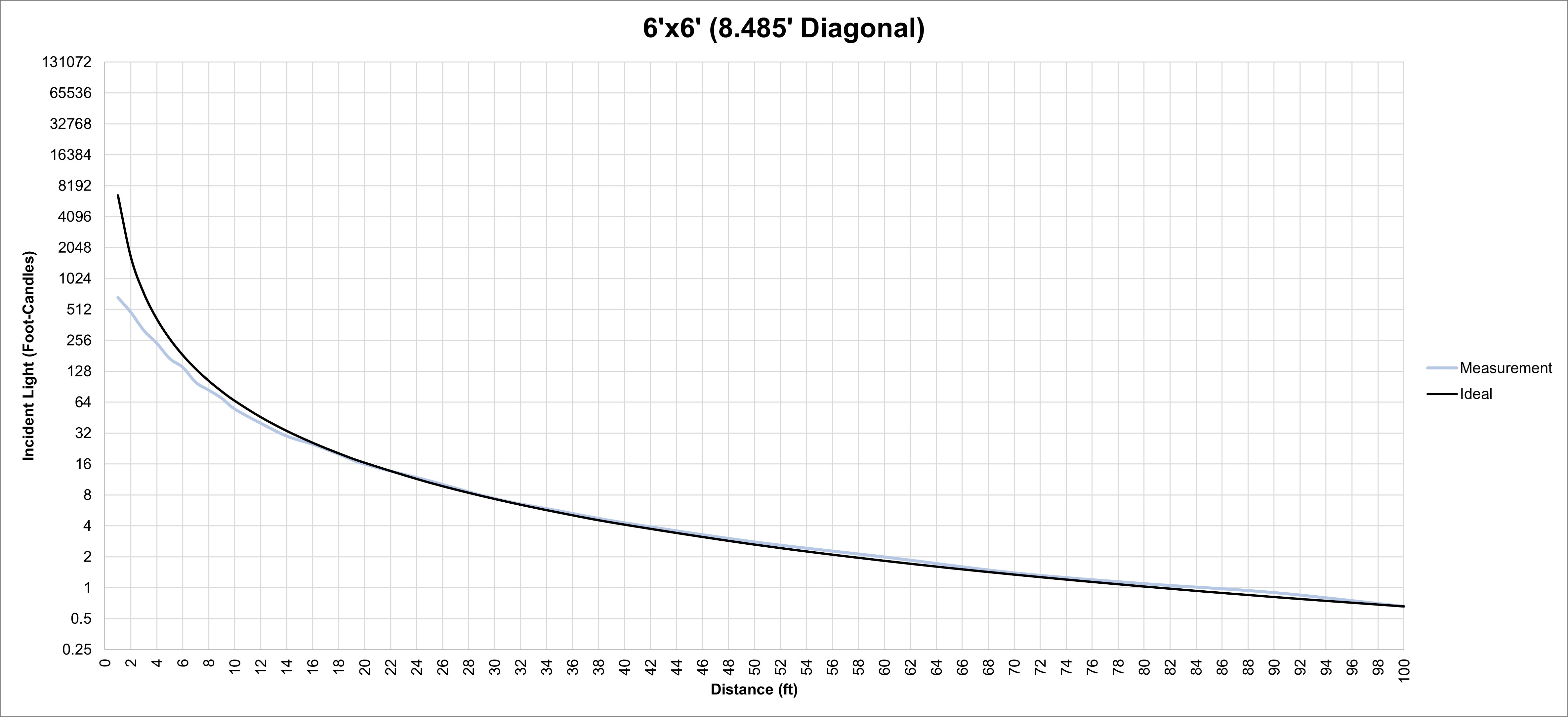
The second shows our measurements from a 6'x6' soft source — a nine-light Maxi-Brute behind a 6'x6' of Full Grid with a 4'x4' of Full Grid between to fully diffuse the source. (In all our tests, we made sure that the face of the diffu-sion was uniformly lit, with no hot spots. This required double-break diffusion.) A 6'x6' square has a diagonal of 8.485'. We can see that our measurements at this distance aren’t on the ideal line, but they’re within 1/6 of a stop, well within an acceptable margin of error. By the time we get to 2x the diagonal distance, the measurement follows the ideal.

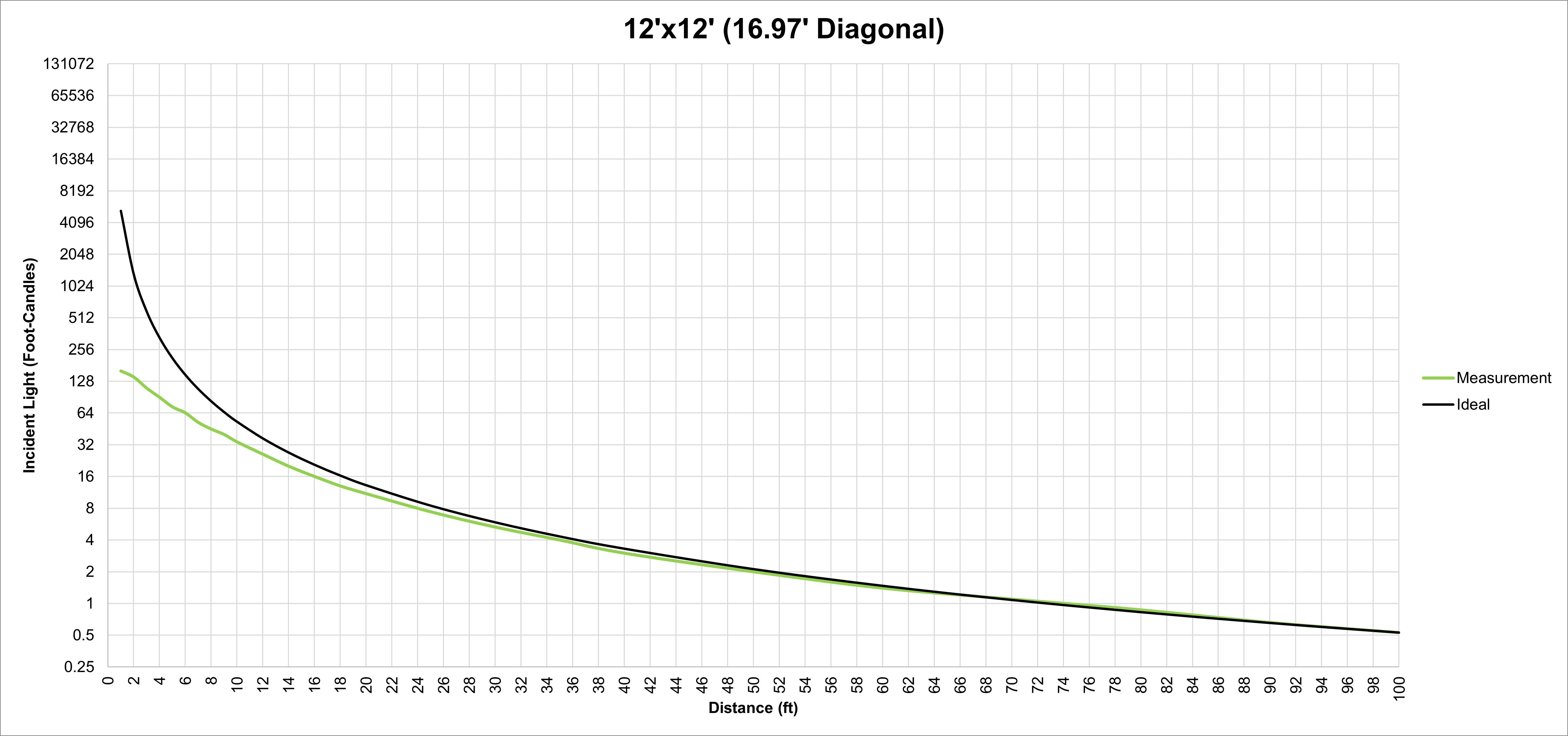
The third shows our measurements from a 12'x12' soft source — the nine-light Maxi-Brute double-broke with 12'x12' Full Grid. At 17' (the diagonal), we’re again within 1/6 of a stop, and at 32' we’re right on the ideal.

The fourth shows our measurements from a 20'x20' soft source — the nine-light Maxi with a 5K tungsten, both double-broke through Full Grid. We struggled with spill from this massive source, and as a result, the measurements aren’t as perfect as we’d hoped, but they serve as a real-world example. From about 30', the diagonal, we’re just within 1/6 of a stop margin of error, but by the time we get to 60', it falls in line exactly with the ideal.

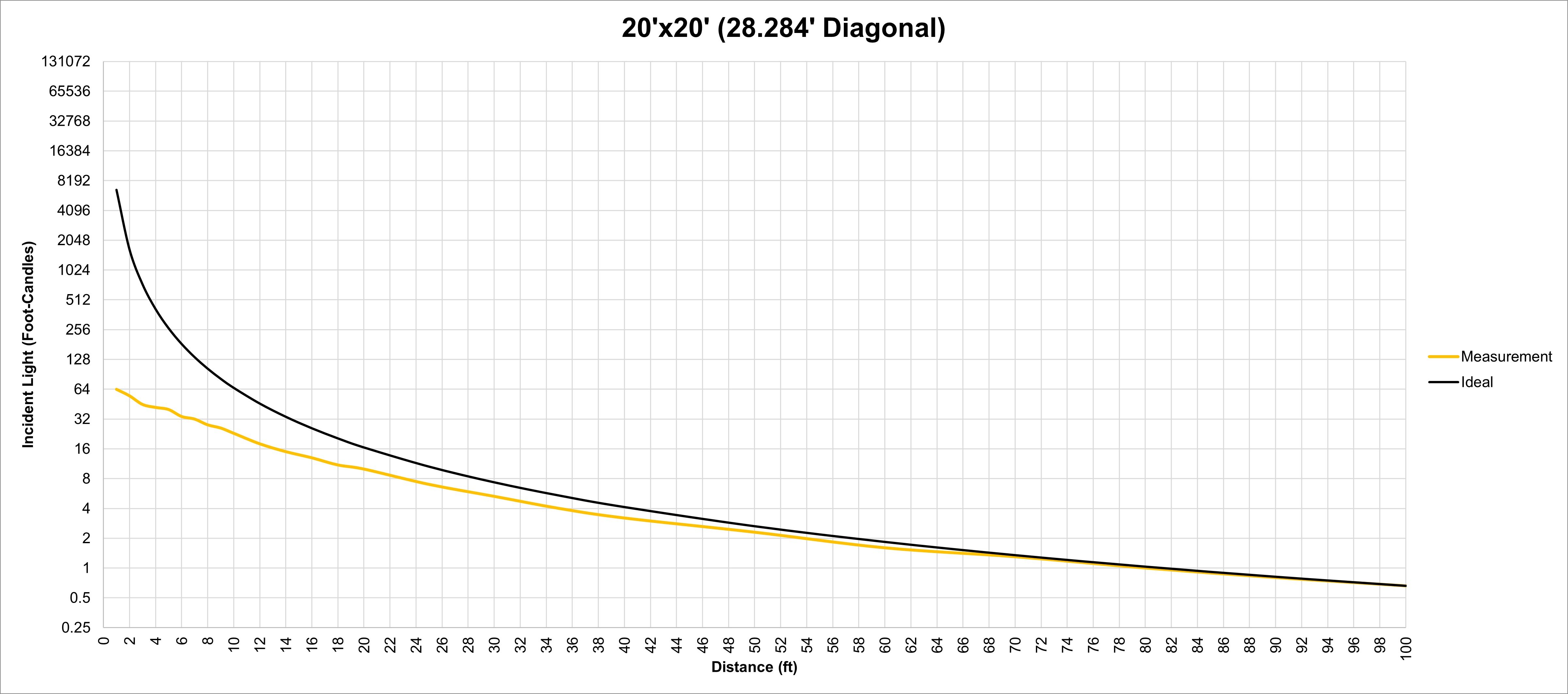
These tests also proved something seasoned gaffers and cinematographers have known for years: Falloff from soft light is significantly less steep than falloff from a point source. You can see that each size soft source has a much more gradual loss of light over the initial distance, and eases into an even more gradual loss over distance. This is another reason why soft light is better for large spaces or large crowds.

It was exciting and deeply satisfying to prove Kang’s theory practically and create a new addendum to cinematog-raphy textbooks everywhere.

Thanks to Tim Kang, Triscenic Production Services, MBS Equipment Co., Mike Visencio and Kaity Williams for their considerable assistance with this test.

Jay Holben is an ASC associate member and AC’s technical editor. He is also the co-author of The Cine Lens Manual.